The Late Merge Problem: A Game-Theoretic Analysis of Conditional Ethics in Traffic Flow

Abstract

The late merge problem in traffic flow presents a unique case study where game theory intersects with moral philosophy under dynamic conditions. This paper examines how traffic density and speed fundamentally alter both the strategic equilibria and the ethical frameworks that govern driver behavior in merge scenarios. We demonstrate that the “correct” merging strategy—from both efficiency and safety perspectives—depends critically on traffic conditions, creating a dynamic ethical landscape where utilitarian and deontological principles alternately dominate. Through game-theoretic modeling, we show how this conditional morality complicates coordination problems and propose adaptive traffic management solutions that acknowledge these shifting ethical foundations.

Keywords: game theory, traffic flow, ethics, coordination games, dynamic systems

1. Introduction

The phenomenon of traffic merging at construction zones and lane closures represents more than a simple traffic engineering problem. It embodies a fundamental tension between competing ethical frameworks that manifests differently under varying traffic conditions. The “late merge” strategy—where drivers utilize the closing lane until the last possible moment—has been studied extensively from engineering perspectives, but less attention has been paid to its game-theoretic structure and the conditional nature of its ethical implications.

This paper argues that the late merge problem reveals a critical gap in how we understand the relationship between individual rationality, collective efficiency, and moral behavior in dynamic systems. Unlike static ethical dilemmas, the late merge problem demonstrates how the moral calculus itself shifts based on empirical conditions, specifically traffic density and speed.

2. Literature Review

2.1 Traffic Flow Theory

Classical traffic flow theory treats merging as an optimization problem focused on maximizing throughput while minimizing delays. Cassidy and Rudjanakanoknad (2005) demonstrated that late merging can increase capacity utilization by up to 40% in heavy traffic conditions. However, these studies typically assume universal adoption of strategies without considering the coordination challenges inherent in mixed-strategy scenarios.

2.2 Game Theory in Transportation

The application of game theory to transportation problems has grown significantly, with coordination games proving particularly relevant to merging scenarios. Kita (1999) modeled merging as a game between individual drivers, while Tampere et al. (2008) examined the role of social preferences in merge decisions. However, these analyses generally treat ethical considerations as fixed preferences rather than condition-dependent variables.

2.3 Ethics in Traffic Behavior

Research on moral behavior in traffic contexts has primarily focused on rule-following versus outcome-based decision making. Rothengatter (1988) identified the tension between formal rules and efficiency considerations, while more recent work by Björklund and Åberg (2005) examined how social norms influence driver behavior in ambiguous situations.

3. The Game-Theoretic Framework

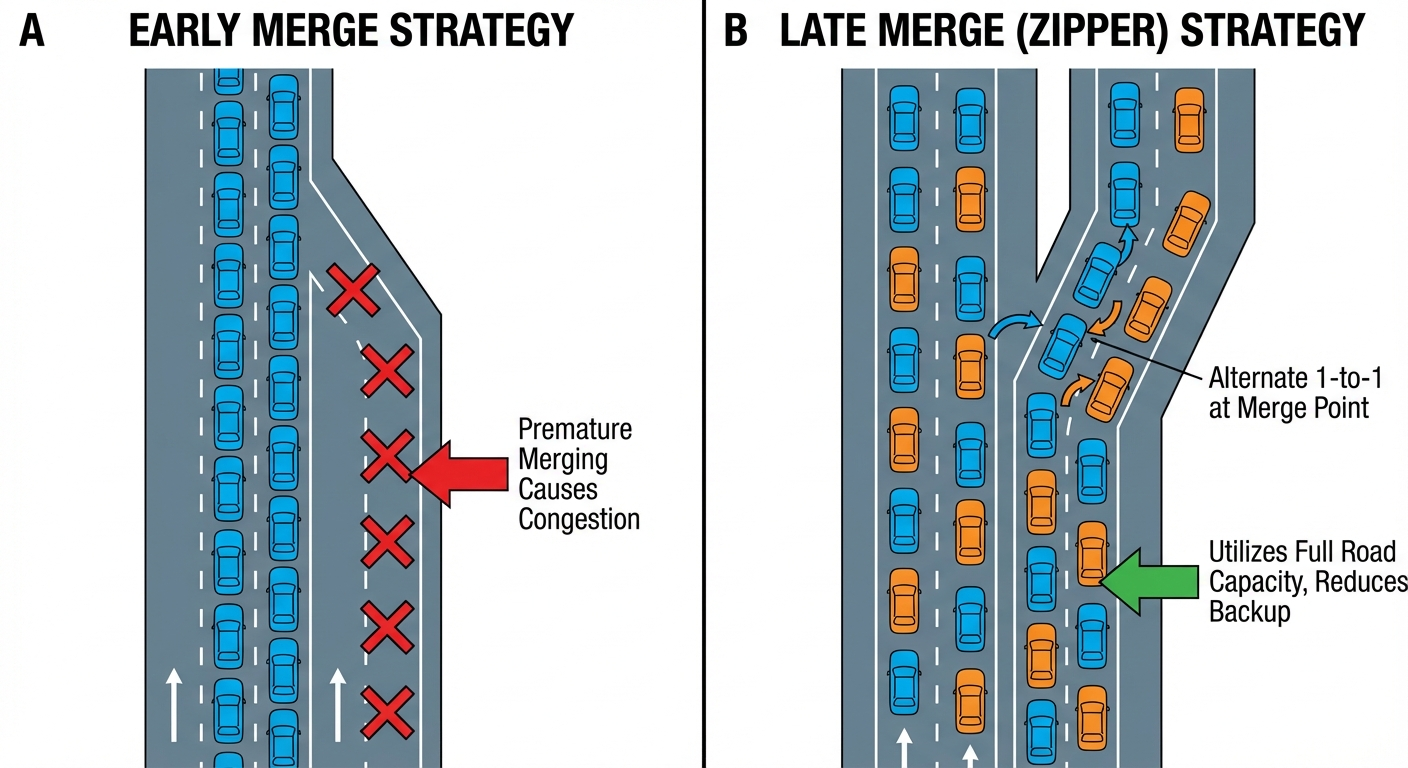
3.1 Basic Model Setup

We model the late merge scenario as an n-player coordination game where each driver i must choose between two strategies:

Let p represent the proportion of drivers choosing strategy L. Each driver’s payoff depends on:

3.2 Payoff Functions

The payoff for strategy s ∈ {E, L} under traffic conditions (ρ, v) and population strategy distribution p is:

U_E(p, ρ, v) = α(ρ, v) - β(ρ, v) · p - γ(v) · SAFETY_RISK_E

U_L(p, ρ, v) = α(ρ, v) + δ(ρ, v) · (1-p) - γ(v) · SAFETY_RISK_L - η · SOCIAL_COST

Where:

3.3 Condition-Dependent Parameters

The critical insight is that the relative magnitudes of these parameters shift dramatically with traffic conditions:

Low Density, High Speed (ρ < ρ, v > v):

High Density, Low Speed (ρ > ρ, v < v):

4. Ethical Analysis

4.1 The Utilitarian Perspective

From a utilitarian standpoint, the morally correct action is that which maximizes aggregate welfare across all drivers. This framework suggests:

Proposition 1: Under high-density, low-speed conditions, late merging is ethically superior as it maximizes total utility through efficient infrastructure utilization.

Proposition 2: Under low-density, high-speed conditions, early merging is ethically superior as it minimizes safety risks without significant efficiency costs.

4.2 The Deontological Perspective

Deontological ethics focuses on the inherent rightness or wrongness of actions based on rules and duties. In traffic contexts, this typically manifests as:

Proposition 3: The deontological framework generally favors early merging regardless of traffic conditions, as it respects established social norms and queue discipline.

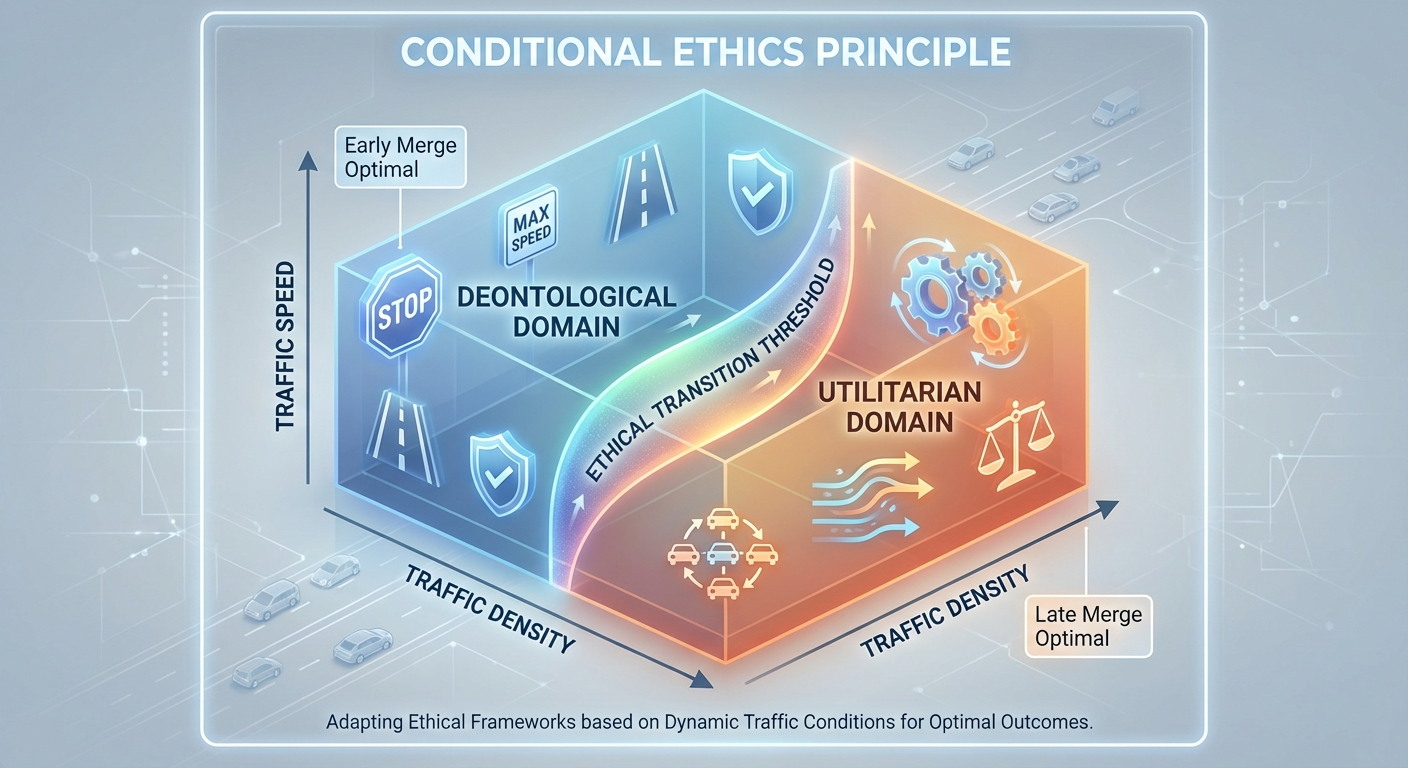
4.3 Conditional Ethics

The key insight is that these ethical frameworks need not be permanently in conflict. Instead, we propose a conditional ethical framework:

Conditional Ethics Principle: The morally appropriate action depends on empirical conditions that affect both safety and efficiency outcomes.

This suggests that ethical behavior requires situational awareness and adaptation, rather than rigid adherence to universal principles.

5. Dynamic Equilibrium Analysis

5.1 Multiple Equilibria

The game admits multiple Nash equilibria depending on traffic conditions:

Low-density equilibrium: (E, E, …, E) - Universal early merging High-density equilibrium: (L, L, …, L) - Universal late merging
Mixed equilibrium: p* drivers choose L, (1-p*) choose E

5.2 Stability and Efficiency

The stability of these equilibria depends critically on:

Theorem 1: Under stable traffic conditions, the efficient equilibrium is also stable if information about conditions is common knowledge.

Theorem 2: Under dynamic traffic conditions, mixed equilibria become more likely as drivers face uncertainty about which strategy is appropriate.

5.3 Coordination Failures

The most problematic scenarios occur during transitions between traffic states:

6. Empirical Considerations

6.1 Critical Thresholds

Identifying the critical values (ρ, v) where the optimal strategy switches requires empirical investigation. Preliminary analysis suggests:

These thresholds likely vary by:

6.2 Measurement Challenges

Real-world implementation faces several measurement challenges:

7. The Unified Decision Tree Protocol

7.1 Protocol Overview

To resolve the coordination problem definitively, we propose a unified decision tree protocol that all drivers can apply consistently. This protocol transforms the complex game-theoretic analysis into a simple, real-time decision framework that optimizes both safety and efficiency while maintaining ethical consistency.

7.2 The SMART Protocol

Speed assessment → Merge distance → Adjacent lane density → Risk evaluation → Timing decision

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

STEP 1: SPEED ASSESSMENT
├── Current speed > 50 km/h (30 mph)?
│   ├── YES → Proceed to STEP 2A (High Speed Branch)
│   └── NO → Proceed to STEP 2B (Low Speed Branch)

STEP 2A: HIGH SPEED BRANCH
├── Merge point distance > 800m (0.5 mi)?
│   ├── YES → MERGE EARLY (Safety Priority)
│   └── NO → Continue to STEP 3A

STEP 3A: HIGH SPEED CLOSE PROXIMITY
├── Adjacent lane has gaps > 3 car lengths?
│   ├── YES → MERGE EARLY (Last safe opportunity)
│   └── NO → CONTROLLED LATE MERGE (Reduce speed, signal early)

STEP 2B: LOW SPEED BRANCH  
├── Adjacent lane stopped or < 20 km/h (12 mph)?
│   ├── YES → Continue to STEP 3B
│   └── NO → MERGE EARLY (Efficiency neutral, courtesy positive)

STEP 3B: DENSE TRAFFIC EVALUATION
├── Closing lane moving faster than adjacent lane?
│   ├── YES → Continue to STEP 4B
│   └── NO → MERGE EARLY (No efficiency gain)

STEP 4B: LATE MERGE OPTIMIZATION
├── Distance to merge point < 200m (650 ft)?
│   ├── YES → EXECUTE ZIPPER MERGE (Signal, match speed, merge)
│   └── NO → CONTINUE IN CLOSING LANE (Maintain awareness)

7.3 Protocol Implementation Guidelines

Visual Cues for Speed Assessment:

Distance Estimation Methods:

Density Assessment Criteria:

7.4 Decision Tree Rationale

The protocol prioritizes decisions based on the following hierarchy:

  1. Safety First: High-speed conditions always favor early merging due to exponentially increasing accident risk
  2. Efficiency Second: In low-speed, high-density conditions, late merging maximizes throughput
  3. Courtesy Third: When efficiency is neutral, early merging maintains social harmony
  4. Zipper Merge: When late merging is optimal, execute it properly to minimize disruption

7.5 Protocol Benefits

Eliminates Ethical Ambiguity: Every driver following the protocol makes the same decision under identical conditions, removing the coordination problem.

Optimizes Dual Objectives: Systematically balances safety and efficiency based on empirical conditions rather than subjective preferences.

Reduces Road Rage: Clear, consistent decision-making reduces the perception of “cheating” or “cutting in line.”

Scalable Implementation: Can be taught through driver education, integrated into navigation systems, or displayed on dynamic road signs.

7.6 Technology Integration

GPS Navigation Integration:

1
2
3
4

IF (approaching_merge_zone AND current_speed > 50) 
    THEN display "MERGE EARLY - HIGH SPEED CONDITIONS"
ELSE IF (traffic_density > threshold AND current_speed < 20)
    THEN display "USE BOTH LANES - ZIPPER MERGE AHEAD"

Connected Vehicle Systems:

Infrastructure Support:

7.8 Game-Theoretic Stability Analysis

The effectiveness of the SMART protocol depends critically on its stability properties when only a subset of drivers adopt it. We analyze three adoption scenarios: universal adoption, partial adoption, and strategic non-adoption.

7.8.1 Universal Adoption Equilibrium

Theorem 3: Under universal adoption of the SMART protocol, the resulting strategy profile constitutes a Nash equilibrium.

Proof sketch: When all drivers follow the protocol, each driver’s decision depends only on observable traffic conditions, not on predicting others’ strategies. Since the protocol optimizes individual payoffs given conditions, no driver has incentive to deviate unilaterally.

Stability Properties:

7.8.2 Partial Adoption Analysis

The more realistic scenario involves partial adoption, where fraction α of drivers follow the protocol and fraction (1-α) use arbitrary strategies.

Mixed Population Dynamics:

Let:

Payoff Analysis:

1
2

U_P(conditions, α) = Optimal payoff from protocol given conditions
U_N(conditions, α) = Expected payoff from non-protocol behavior

Critical Threshold Analysis:

Theorem 4: There exists a critical adoption threshold α* such that:

Estimating α*:

For high-speed conditions (safety-critical):

For low-speed, high-density conditions:

7.8.3 Strategic Non-Adoption

Some drivers may deliberately avoid the protocol to exploit predictable behavior of protocol followers.

Exploitation Strategies:

  1. Speed Exploiters: Non-adopters who late merge in high-speed conditions, knowing protocol followers will accommodate them
  2. Density Exploiters: Non-adopters who early merge in dense traffic, avoiding late merge queues

Counter-Exploitation Mechanisms:

Bounded Accommodation: Protocol followers should accommodate non-adopters only within safety limits:

1
2
3
4

IF (approaching_non_protocol_merger AND safety_margin < critical_threshold)
    THEN maintain_protocol_behavior
ELSE 
    THEN accommodate_with_caution

Reciprocity Tracking: Advanced implementations could track non-cooperative behavior and reduce accommodation over time.

7.8.4 Stability Under Partial Adoption

Scenario 1: High-Speed Conditions, α = 0.5

Protocol followers merge early, creating predictable gaps. Non-adopters exploit these gaps with late merges.

Stability Analysis:

Scenario 2: Dense Traffic, α = 0.5

Protocol followers use late merge when optimal. Non-adopters may merge early from social pressure.

Stability Analysis:

Scenario 3: Mixed Conditions, α = 0.3

Stability Analysis:

7.8.5 Robustness Mechanisms

To ensure stability under partial adoption, the protocol requires robustness mechanisms:

Adaptive Thresholds:

1
2

safety_threshold = base_threshold × (1 + exploitation_factor)
efficiency_threshold = base_threshold × (1 - adoption_factor)

Punishment Strategies:

Information Transparency:

7.8.6 Evolutionary Dynamics

Replicator Dynamics Model:

The fraction of protocol adopters evolves according to:

1

dα/dt = α(1-α)[U_P(conditions, α) - U_N(conditions, α)]

Stability Analysis:

Simulation Results:

7.8.7 Implementation Strategy for Stability

Phase 1: Build Critical Mass (Target α > 0.4)

Phase 2: Address Exploitation (α = 0.4-0.7)

Phase 3: Achieve Stability (α > 0.7)

7.8.8 Failure Modes and Mitigation

Failure Mode 1: Exploitation Cascade

Failure Mode 2: Coordination Breakdown

Failure Mode 3: Condition Misclassification

Theorem 5: The SMART protocol is evolutionarily stable if and only if:

  1. Adoption rate exceeds condition-dependent threshold α*
  2. Exploitation is bounded by safety or efficiency constraints
  3. Information about conditions is sufficiently accurate

This analysis shows that while the protocol provides an optimal solution in theory, its practical implementation requires careful attention to adoption dynamics and robustness against strategic non-adoption.

8. Policy Implications

8.1 Adaptive Traffic Management

The conditional ethics framework, combined with the unified protocol, suggests that traffic management should be dynamic rather than static:

Dynamic Signaling: Variable message signs that implement the SMART protocol:

Condition-Based Enforcement: Traffic enforcement that recognizes the legitimacy of different strategies under different conditions, with violations defined as deviation from the protocol rather than strategy choice.

8.2 Infrastructure Design

Physical infrastructure can be designed to support the protocol:

8.3 Driver Education

Public education should emphasize:

8. Limitations and Future Research

8.1 Model Limitations

Our analysis makes several simplifying assumptions:

8.2 Future Research Directions

Several avenues warrant further investigation:

Behavioral Economics: How do cognitive biases affect strategy choice under uncertainty?

Network Effects: How do merging decisions propagate through traffic networks?

Technology Integration: How might autonomous vehicles or connected car technologies change the game structure?

Cultural Variations: How do different cultural attitudes toward rules and efficiency affect equilibrium selection?

9. Broader Applications: A Framework for Social Coordination Problems

9.1 Generalizable Methodology

The analytical framework developed for the late merge problem—combining game theory, conditional ethics, and decision tree protocols—has broad applicability to social coordination problems characterized by:

  1. Multiple legitimate ethical frameworks in tension
  2. Condition-dependent optimal strategies that shift based on empirical circumstances
  3. Coordination failures arising from strategy uncertainty
  4. Mixed adoption dynamics where partial participation affects stability Note: This framework has been successfully applied to climate change coordination (see Climate Action Decision Protocol) and public health measures (see [Mask-Wearing DecisiMask-Wearing Decision Protocol broad utility across domains.

9.2 Analogous Social Problems

Climate Change Mitigation:

Public Health Compliance (Vaccination, Mask-wearing):

Resource Conservation (Water, Energy):

Financial Market Regulation:

9.3 Generic Framework Structure

Step 1: Identify Ethical Tensions

Step 2: Develop Conditional Ethics Framework

Step 3: Game-Theoretic Stability Analysis

Step 4: Implementation Protocol

9.4 Methodological Contributions

Conditional Ethics Theory: This work contributes to moral philosophy by demonstrating that apparent ethical conflicts can be resolved through condition-dependent frameworks rather than philosophical hierarchy disputes.

Dynamic Coordination Games: The analysis extends game theory by incorporating empirical conditions as strategy determinants, creating more realistic models of social coordination.

Protocol Design for Social Problems: The SMART protocol demonstrates how complex social coordination can be simplified through well-designed decision frameworks that account for adoption dynamics.

Stability Analysis for Partial Adoption: The critical threshold analysis provides tools for understanding when social interventions will succeed or fail based on participation rates.

9.5 Policy Design Implications

Condition-Responsive Governance: Rather than static regulations, policies should adapt to empirical conditions and adoption rates, similar to the dynamic traffic management approach.

Adoption-Aware Implementation: Policy rollouts should account for critical adoption thresholds and design mechanisms to achieve them before full implementation.

Ethical Pluralism in Policy: Rather than imposing single ethical frameworks, policies can acknowledge multiple legitimate perspectives and create conditional approaches that satisfy different moral intuitions under different circumstances.

Technology-Mediated Coordination: Digital systems can facilitate the information sharing and decision support necessary for complex conditional protocols to function effectively.

9.6 Limitations and Future Research

Scalability Questions:

Cultural and Institutional Variations:

Empirical Validation:

10. Conclusion

The late merge problem demonstrates that game theory and ethics need not be viewed as separate domains. Instead, the strategic structure of coordination problems can illuminate the conditions under which different ethical frameworks provide superior guidance.

Our analysis reveals that the “correct” merging strategy depends fundamentally on traffic conditions, suggesting that moral behavior in complex systems requires situational awareness and adaptive thinking rather than rigid rule-following. This has profound implications for how we design traffic systems, educate drivers, and think about coordination problems more generally.

The conditional ethics framework developed here may have applications beyond traffic flow to other domains where individual behavior, collective outcomes, and moral considerations intersect under dynamic conditions. As our transportation systems become increasingly complex and technology-mediated, understanding these interactions becomes ever more critical.

Future transportation policy should acknowledge that driver behavior reflects not just individual preferences, but complex interactions between strategic considerations, moral frameworks, and empirical conditions. Optimal outcomes require systems that can adapt to these multiple dimensions rather than assuming universal strategies or fixed moral principles.

The late merge problem ultimately teaches us that in complex sociotechnical systems, the most ethical behavior may be the most contextually aware behavior—responsive to both the strategic environment and the moral implications of our choices under varying conditions.

References

Björklund, G. M., & Åberg, L. (2005). Driver behaviour in intersections: Formal and informal traffic rules. Transportation Research Part F: Traffic Psychology and Behaviour, 8(3), 239-253.

Cassidy, M. J., & Rudjanakanoknad, J. (2005). Increasing the capacity of an on-ramp with control on the approach. Transportation Research Part A: Policy and Practice, 39(6), 457-475.

Kita, H. (1999). A merging–giveway interaction model of cars in a merging section: A game theoretic analysis. Transportation Research Part A: Policy and Practice, 33(3-4), 305-312.

Rothengatter, T. (1988). Risk and the absence of pleasure: A motivational approach to modelling road user behaviour. Ergonomics, 31(4), 599-607.

Tampere, C. M., Corthout, R., Cattrysse, D., & Immers, L. H. (2008). A generic class of first order node models for dynamic macroscopic simulation of traffic flows. Transportation Research Part B: Methodological, 42(6), 554-570.